Solution:
(i) Let p(x) = x3 - 2x2 - x + 2
By the factor theorem we know that x - a is a factor of p (x) if p (a) = 0.
We shall find a factor of p(x) by using some trial value of x, say x = 1.
p(1) = (1)3 - 2(1)2 - 1 + 2
= 1 - 2 - 1 + 2 = 0
Since the remainder of p(1) = 0 , by factor theorem we can say p(x) = x3 - 2x2 - x + 2 is divisible by x - 1.
Now divide p(x) by x - 1 using long division,
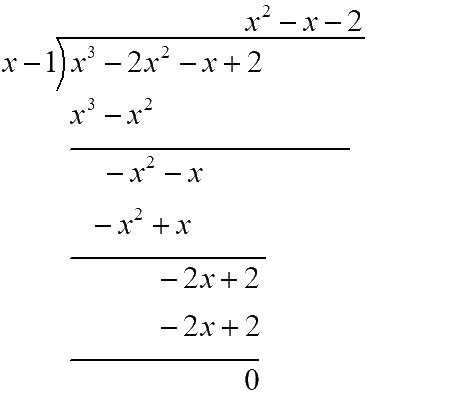
Hence x3 - 2x2 - x + 2 = (x -1) (x2 - x - 2)
Now taking x2 - x - 2 , find two numbers p, q such that:
p + q = co-efficient of x
p × q = product of co-efficient of x2 and the constant term
p + q = -1 (co-efficient of x)
p × q = 1 × (-2) = -2 (co-efficient of x2 and the constant term.)
By trial and error method, we get p = -2, q = 1.
Now splitting the middle term of the given polynomial,
x2 - x - 2 = x2 - 2x + x - 2
= x(x - 2) + 1(x - 2)
= (x + 1) (x - 2)
∴ x3 - 2x2 - x + 2 = (x - 1) (x - 2) (x + 1)
Method 2:
x3 - 2x2 - x + 2 = (x3 - 2x2) - (x - 2)
= x2 (x - 2) - 1(x - 2)
= (x - 2) (x2 -1)
= (x - 2) (x + 1) (x - 1) (By using a2 - b2 = (a + b)(a - b) )
(ii) Let p(x) = x3 - 3x2 - 9x - 5
We shall find a factor of p(y) by using some trial value of y, say x = -1
p(-1) = (-1)3 - 3(-1)2 - 9(-1) - 5
= -1 - 3 + 9 - 5
= -9 + 9 = 0
Since the remainder of p(-1) = 0 , by factor theorem we can say x + 1 is a factor ofp(x) = x3 - 3x2 - 9x - 5.
Now dividing p(x) by x + 1 using long division.

Hence x3 - 3x2 - 9x - 5 = (x +1) (x2 - 4x - 5)
Now taking x2 - 4x - 5, find two numbers p, q such that:
p + q = -4 (co-efficient of x)
p × q = 1 × -5 = -5 (product of co-efficient of x2 and the constant term)
By trial and error method, we get p = -5, q = 1.
Now splitting the middle term of the given polynomial,
x2 - 4x - 5 = x2 - 5x + x - 5
= x(x - 5) + 1(x - 5)
= (x + 1)(x - 5)
Therefore, x3 - 3x2 - 9x - 5 = (x + 1) (x - 5) (x + 1) = (x + 1)2 (x - 5)
(iii) Let p(x) = x3 + 13x2 + 32x + 20
We shall find a factor of p(x) by using some trial value of x, say x = -1. (Since all the terms are positive.)
p(-1) = (-1)3 + 13(-1)2 + 32(-1) + 20
= -1 + 13 - 32 + 20 = 0
Since the remainder of p(-1) = 0, by factor theorem we can say x + 1 is a factor of p(x) = x3 + 13x2 + 32x + 20.
Now dividing p(x) by x + 1 using long division,

Therefore, x3 + 13x2 + 32x + 20 = (x + 1)(x2 + 12x + 20)
Now taking x2 + 12x + 20, find two numbers p, q such that:
p + q = 12 (co-efficient of x)
p × q = 1 × 20 = 20 (product of co-efficient of x² and the constant term.)
By trial and error method, we get p = 10, q = 2.
Now splitting the middle term of the given polynomial,
x2 + 12x + 20 = x2 + 10x + 2x + 20
= x(x + 10) + 2(x + 10)
= (x + 10) (x + 2)
Therefore, x3 + 13x2 + 32x + 20 = (x + 1) (x + 10) (x + 2)
Method 2:
x3 + 13x2 + 32x + 20 = x3 + 10x2 + 3x2 + 30x + 2x + 20
= x2 (x + 10) + 3x(x + 10) + 2(x + 10)
= (x + 10) (x2 + 3x + 2)
= (x + 10) (x2 + 2x + x + 2)
= (x + 10) [x(x + 2) + 1(x + 2)]
= (x + 10) (x + 2) (x + 1)
(iv) Let p(x) = 2y3 + y2 - 2y - 1
We shall find a factor of p(y) by using some trial value of y, say y = 1.
p(1) = 2(1)3 + (1)2 - 2(1) - 1
= 2 + 1 - 2 - 1 = 0
Since the remainder of p(1) = 0, by factor theorem we can say y - 1 is a factor of p(y) = 2y3 + y2 - 2y - 1
Now dividing p(y) by y - 1 using long division,

Therefore, 2y3 + y2 - 2y - 1 = (y - 1) (2y2 + 3y + 1)
Now taking 2y2 + 3y + 1, find two numbers p, q such that:
p + q = 3 (co-efficient of y)
p × q = 2 × 1 = 2 (product of co-efficient of y2 and the constant term)
By trial and error method, we get p = 2, q = 1.
Now splitting the middle term of the given polynomial,
2y2 + 3y + 1 = 2y2 + 2y + y + 1
= 2y(y + 1) + 1 (y + 1)
= (2y + 1) (y + 1)
Therefore, 2y3 + y2 - 2y - 1 = (y - 1) (2y + 1) (y + 1)
☛ Check: NCERT Class 9 Maths Solutions Chapter 2
Video Solution:
Factorise: (i) x³ - 2x² - x + 2 (ii) x³ - 3x² - 9x - 5 (iii) x³ + 13x² + 32x + 20 (iv) 2y³ + y² - 2y - 1
NCERT Solutions Class 9 Maths Chapter 2 Exercise 2.4 Question 5:
Summary:
The factorized form of x3 - 2x2 - x + 2, x3 - 3x2 - 9x - 5, x3 + 13x2 + 32x + 20, 2y3 + y2 - 2y - 1 are (x - 1)(x - 2)(x + 1), (x + 1)2(x - 5), (x + 10)(x + 2)(x + 1) and (y - 1)(2y + 1)(y + 1) respectively.
☛ Related Questions:
- Determine which of the following polynomials has (x + 1) a factor:i) x3 + x2 + x + 1ii) x4 + x3 + x2 + x + 1iii) x4 + 3x3 + 3x2 + x +1iv) x3 - x2 - (2 + √2)x + √2
- Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:(i) p(x) = 2x3 + x2 - 2x - 1, g(x) = x +1(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2(iii) p(x) = x3 - 4x2 + x + 6, g(x) = x - 3
- Find the value of k, if x - 1 is a factor of p(x) in each of the following cases: (i) p(x) = x2 + x + k (ii) p(x) = 2x2 + kx + √2 (iii) p(x) = kx2 - √2x + 1 (iv) (x) = kx2 - 3x + k


