Tính Nguyên Hàm Của Tanx Bằng Công Thức Cực Hay

1. Nguyên hàm (tanx-cotx)^2

Bài tập 1: Tính nguyên hàm của f(x)= tanx - cotx$frac{1}{2}$

Giải:

Dùng kỹ thuật thêm bớt, ta được:

$int tan^{2}xdx= left [ left ( 1+tan^{2}x right )-1 right ]dx$

=$int left ( 1+tan^{2}x right )dx-int dx$

=$int frac{1}{cos^{2}x}dx-int dx$

=$tanx-x+C$

Bài tập 2: Tìm các nguyên hàm sau

a) I= $int sin5xcos2xdx$.

b) I= $int sin3xsin6xdx$.

c) I= $int sin2xcos3xdx$.

d) I= $int cosxcos3xdx$.

Giải:

Tham khảo thêm bài tập nguyên hàm $left (tanx-cotx right )^{2}$ tại đây

2. Nguyên hàm tanx dx

Bài tập 1: Tính nguyên hàm của f(x)= $int tanxdx$

Giải

Ta có

$int tanxdx=int frac{sinx}{cosx}dx= -int frac{1}{cosx}d(cosx)= -lnleft | cosx right | +C$

Bài tập 2: Tính các nguyên hàm sau:

e) I = $int cosxcos3xcos5xdx$. f) I = $int sinxsin3xsin5xdx$. g) I = $int sinxcos3xcos5xdx$. h) I = $int cosxsin3xsin5xdx$.

Giải:

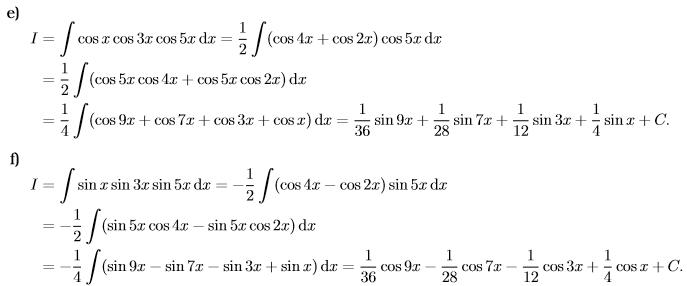
3. Tìm nguyên hàm của (tanx+cotx)^2

Bài tập 1: Nghiệm của phương trình tanx + cotx = -2 là

Giải:

Bài tập 2: Tính nguyên hàm F(x)= $int sin^{2}2xdx$

Giải:

Ta có

F(x)= $int sin^{2}2xdx= int frac{1-cos4x}{2}dx= frac{1}{2}int 1dx - frac{1}{2}int cos4xdx= frac{1}{2}x - frac{1}{8}sin4x + C$

Bài tập 3: Tính nguyên hàm f(x)= $frac{1}{sin^{2}x.cos^{4}x}$

Giải:

Đặt

t= tanx

$Leftrightarrow dt= frac{dx}{cos^{2}x}$; $1+tan^{2}x= frac{1}{cos^{2}x}$ $Leftrightarrow frac{1}{cos^{2}x}= t^{2}+1$ $Leftrightarrow cos^{2}x= frac{1}{t^{2}+1}$ $Rightarrow sin^{2}x= frac{t^{2}}{t^{2}+1}$

Khi đó:

$int fleft ( x right )dx= int frac{1}{sin^{2}xcos^{2}x}.frac{dx}{cos^{2}x}$ = $int frac{(t^{2}+1)^{2}}{t^{2}}dt= int(t^{2}+frac{1}{t^{2}}+2)dt$ = $frac{t^{3}}{3} - frac{1}{t} + 2t + C$

Vậy, $int f(x)dx= frac{tan^{3}x}{3} + 2tanx - frac{1}{tanx} + C$

4. Nguyên hàm của tanx.sin2x

Bài tập 1: Giải phương trình sau: tanx.sin2x - 2sin2x = 3(cos2x + sinx.cosx)

Bài tập 2: Tìm nguyên hàm của hàm số f(x) = sin (2x-1)

Giải:

Ta có:

$int f(x)dx= int sin(2x-1)dx= frac{1}{2}int sin(2x-1)d(2x-1)= frac{-1}{2}cos(2x-1) + C$

Ví dụ 3: Tính nguyên hàm

J=(cos3x.cos4x+sin32x)dx

Giải:

Ví dụ 3: Tính nguyên hàm F(x)= sin22xdx

Giải

F(x)= $int sin^{2}2xdx= int frac{1-cos4x}{2}dx= frac{1}{2}int 1dx - frac{1}{2}cos4xdx$ = $frac{1}{2}x - frac{1}{8}int cos4xd(4x)= frac{1}{2}x - frac{1}{8}sin4x + C$

5. Nguyên hàm sin^2x.tanx

Bài tập 1: Một nguyên hàm F(x) của hàm số f(x) = tanx.sin2x thỏa mãn điều f ($frac{Pi }{4})=0$

Giải:

$int tanx.sin2xdx= int (1-cos2x)dx= x - frac{1}{2}x + C$ $Rightarrow F(x)= x - frac{1}{2}sin2x + C$

F$(frac{pi }{4}) Leftrightarrow C= frac{1}{2}-frac{pi}{4}$

Vậy f(x) = x - $frac{1}{2}sin2x + frac{1}{2} - frac{pi }{4}$

Bài tập 2: Tính nguyên hàm của f(x)=4x+sin3x

Giải

Ví dụ 3: Tìm nguyên hàm f(x)= (sin+cosx)3

Giải

$int (sinx+cosx)^{2}dx$ = $int (sin^{2}x+cos^{2}x+2sinxcosx)dx$ = $int (1+sin2x)dx = x - frac{1}{2}cos2x + C$

6. Nguyên hàm 7e^x-tanx

Bài tập 1: Tính nguyên hàm của hàm số F(x)=7$e^{x}−tanx$

Giải

Ta có f’(x)= 7$e^{x} - frac{1}{cos^{2}x} = e^{x}(7-frac{e^{x}}{cos^{2}x})$

Ngoài ra có thể tham khảo thêm một số bài tập nguyên hàm tại đây

Bài tập 2: Tính nguyên hàm f(x)= $e^{x}(3+e^{-x})fx$

Giải

F(x)= $int e^{x}(3+e^{-x})dx = int (3e^{x}+1)dx=3e^{x}+x+C

Bài tập 3: Tìm nguyên hàm y= $x^{2} -3x+frac{1}{x}$

Giải

Sử dụng bảng nguyên hàm nên

$int (x^{2}-3x+frac{1}{x}dx) = frac{x^{3}}{3}-frac{3}{2}x^{2} +lnleft | x right | + C$

7. Nguyên hàm của (tanx)^4

Bài tập 1: Tính nguyên hàm $int tan^{4x}dx$

Giải:

Ta có:

Đặt tanx= t $Rightarrow frac{dx}{tan^{2}x}= dt$

$Rightarrow (tan^{2}x+1)dx= dt Rightarrow dx= frac{dt}{t^{2}+1}$

Bài tập 2: Tìm nguyên hàm f(x) = sin2x

Giải:

Ta có:

$int sin2xdx = frac{1}{1}sin2xd(2x)= frac{-1}{2}cos2x + C$

Bài tập 3: Tìm nguyên hàm f(x)= 1+ $tan^{2}frac{x}{2}$

Giải:

Ta có f(x)= $1+tan^{2}frac{x}{2}= frac{1}{cos^{2}frac{x}{2}}$

Nên $int frac{dx}{cos^{2}frac{x}{2}}= 2int frac{d(frac{x}{2})}{cos^{2}frac{x}{2}} = 2tanfrac{x}{2} + C$

8. Nguyên hàm tan x/cos^2x

Bài tập 1: Tính nguyên hàm f(x)= $frac{1}{cos^{2}x}$

Giải

Bài tập 2: Tìm nguyên hàm của các hàm số

a) $int sin5xsin2xdx$ b) $int 4cos^{2}xdx$ c) $int frac{1}{4cos^{4}x$-$4cos^{2}x+1}$

Giải:

9. Tính nguyên hàm 1/1+tanx

Bài tập 1: Tìm nguyên hàm f(x)= 1+ $tan^{2}frac{x}{2}$

Giải:

f(x)= 1 + $tan^{2}frac{x}{2}= frac{1}{cos^{2}frac{x}{2}}$

Nên $int frac{dx}{cos^{2}frac{x}{2}}= 2int frac{d(frac{x}{2})}{cos^{2}frac{x}{2}}$=

$2tanfrac{x}{2} + C$

Bài tập 2: Tìm nguyên hàm $int(2cosx - 3cos5x)dx$

Giải:

Ta có $int(2cosx-3cos5x)dx = 2sinx-frac{3}{5}x + C$

Bài tập 3: Tính nguyên hàm của $int(sin3x.cos5x) dx$

Giải:

Ta có $int sin3xcos5xdx= frac{1}{2}int (sin8x-sin2x)dx$

= $frac{1}{2}(-frac{cos8x}{8}+frac{cos2x}{2})+C$

10. Nguyên hàm của (tanx)^3

Bài tập 1: Tính nguyên hàm: $I_{3}= int tan^{3}xdx$

Giải:

Bài tập 2: Tính nguyên hàm sau: (sinx - cosx) sinxdx

Giải

11. Nguyên hàm 1+tanx/cos^2x

Bài tập 1: Tính nguyên hàm f(x)= $int frac{x}{cos^{2}x}dx$

Giải:

Sử dụng phương pháp nguyên hàm từng phần với u=x, du= $frac{x}{cos^{2}x}dx$

Phương pháp trắc nghiệm:

Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) - f(x) = 0

Nhập máy tính $frac{d}{dx}$((F(x)) - f(x) . CALC x tại một số giá trị ngẫu nhiên $x_{0}$ trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.

Bài tập 2: Tính nguyên hàm của $int (sin3x.cos5x)dx$

Giải:

Ta có $int sin3xcos5xdx = frac{1}{2}int (sin8x-sin2x)dx$

= $frac{1}{2}(-frac{cos8x}{8}+frac{cos2x}{2}) + C$

12. Nguyên hàm 1/tanx

Bài tập 1: Tính nguyên hàm $frac{1}{tanx}= Cotx$

Giải:

Ta có

$Leftrightarrow frac{1}{frac{sinx}{cosx}}= frac{cosx}{sinx} Leftrightarrow frac{cosx}{sinx} = frac{cosx}{sinx}$

$frac{1}{tanx}= Cotx$

ĐK: $sinxneq 0$ $Leftrightarrow xneq kpi $

Bài tập 2: Tính nguyên hàm $int frac{1}{sin^{2}xcos^{2}x}$

Giải:

Bài tập 3: Tính nguyên hàm f(x) = sin2x

Giải:

$int sin2xdx= frac{1}{2}int sin2xd(2x)= frac{-1}{2}cos2x + C$

13. Nguyên hàm tanx + tan^3x

Bài tập 1: Tính nguyên hàm f(x)= $tan^{3}x$

Giải:

Bài tập 2: Tính nguyên hàm $int tan^{2}xdx$

Giải:

Từ $tan^{2}x= tanx(1+tan^{2}x)- tanx$

Suy ra $int tan^{2}xdx= int tanxd(tanx)+int frac{d(cosx)}{cosx}= frac{tan^{2}x}{2}+lnleft | cosx right | + C$

Bài tập 3: Tính nguyên hàm f(x)= sin2x.tanx

Giải:

14. Nguyên hàm tanx/cos^2x

Bài tập 1: Tính nguyên hàm y= $frac{3+tanx}{cos^{2}x-sin^{2}x} = frac{3+tanx}{cos2x}$

Giải

y= $frac{3+tanx}{cos^{2}x-sin^{2}x} = frac{3+tanx}{cos2x}$

= $frac{3+frac{sinx}{cosx}}{cos2x}= frac{3cosx+sinx}{cos2xcosx}$

Điều kiện: $cos2x.cosxneq 0$

$Leftrightarrow cos2xneq 0 hoặc cosxneq 0$

$Leftrightarrow x=frac{pi }{4}+frac{kpi }{2} hoặc x=frac{pi }{2}+kpi$

Bài tập 2: Tính nguyên hàm $int frac{1}{sin^{2}x-cos^{2}x}$

Giải:

Ta có: $int frac{1}{sin^{2}xcos^{2}x}dx= int frac{sin^{2}x+cos^{2}x}{sin^{2}xcos^{2}x}dx= int (frac{1}{cos^{x}}+frac{1}{sin^{2}x})dx=tanx-cotx+C$

Bài tập 3: Tính nguyên hàm (sinx - cosx)sinxdx

Giải:

Ta có:

$int (sinx-cosx)sinxdx)= int (sin^{2}x-sinxcosx)dx= int (frac{1-cos2x}{2}-frac{sin2x}{2})dx=frac{1}{2}(x-frac{1}{2}sin2x+frac{1}{2}cos2x) +C$

15. Nguyên hàm arctan(tanx)

Bài tập 1: Tính nguyên hàm f(y)=arctanx

Giải:

Ta có: tanx = -√2

x = arctan(-√2) + kπ

(k € Z)

Bài tập 2: Tính nguyên hàm $int (1+2sinx)^{2}$

Giải:

Ta có:

$int (1+2sinx)^{2}dx= int (1+4sinx+4sin^{2}x)dx=int (1+4sinx+4.frac{1-cos2x}{2})dx = int (3+4sinx-2cos2x)dx=3x-4cosx-sin2x+C$

Bài tập 3: Tính nguyên hàm $int cos^{3}xdx$

Giải:

Ta có:

$int cos^{3}dx=frac{1}{4}int (3cosx+cos3x)dx= frac{1}{4}int (3sinx+frac{1}{3}sin3x)+C= sinx -frac{1}{3}sin^{3}x+C$

Ngoài ra các em có thể xem toàn bộ bài giảng về nguyên hàm tanx tại đây nhé!

Sau bài viết này, hy vọng các em đã nắm chắc được toàn bộ lý thuyết, công thức về nguyên hàm tanx, từ đó vận dụng hiệu quả vào bài tập. Để có thêm nhiều kiến thức và các dạng toán hay, các em có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ để có được kiến thức tốt nhất chuẩn bị cho kỳ thi đại học sắp tới nhé!

>> Xem thêm:

• Tích phân là gì? Phương pháp tính và các dạng toán cơ bản
• Bảng công thức tính nguyên hàm đầy đủ nhất - toán lớp 12
• Đầy đủ và chi tiết bài tập phương trình logarit có lời giải