Tích Phân Là Gì? Phương Pháp Tính Tích Phân Và Các Dạng Toán Cơ Bản

1. Tích phân là gì?

Tích phân là một khái niệm sử dụng nhiều trong toán 12 cùng với nghịch đảo của nó là vi phân. Chúng có vai trò quan trọng là 2 phép tính cơ bản, chủ chốt trong lĩnh vực giải tích. Theo tiếng Hán Việt, tích được hiểu là tích cóp còn phân có nghĩa là từng phần nhỏ. Như vậy ta có thể hiểu đơn giản rằng tích phân là tổng của nhiều phần nhỏ. Trong toán học thì tích phân được định nghĩa như sau:

Cho hàm f(x) liên tục trên một khoảng xác định (kí hiệu: K) và a,b là hai số thực bất kì thuộc K. Nếu F(x) là một nguyên hàm của f(x) thì hiệu số của F(b)-F(a) được gọi là tích phân của f(x) trong khoảng (a,b). Từ đó, ta có ký hiệu như sau:

Tích phân từ a đến b của f(x) được ký hiệu là: $int_{a}^{b}f(x)dx$

Ta có: $int_{a}^{b}f(x)dx=F(b)-F(a)$ (với F(x) là một nguyên hàm của f(x))

Trong đó

• ∫: tích phân

• dx: biến của tích phân.

• f(x)dx: biểu thức dưới dấu tích phân

2. Tính chất của tích phân xác định

Để thành thạo các phương pháp giải tích phân để áp dụng giải bài tập, các bạn học sinh cùng VUIHOC điểm qua một số những tính chất của tích phân thường gặp nhé!

(1) Tích phân tại một giá trị xác định của biến số thì bằng 0

$int_{a}^{a}f(x)=0$

(2) Đảo cận thì đổi dấu

$int_{a}^{b}f(x)dx=-int_{b}^{a}f(x)dx$

(3) Hằng số trong tích phân có thể được đưa ra ngoài dấu tích phân

$int_{b}^{a}k times f(x)dx=ktimesint_{a}^{b}f(x)dx$

(4) Tích phân một tổng bằng tổng các tích phân

$int_{a}^{b}[f_{1}(x)pm f_{2}(x)pm...pm f_{n}(x)]dx=int_{a}^{b}f_{1}(x)dxpmint_{a}^{b}f_{2}(x)dxpm...pmint_{a}^{b}f_{n}(x)dx$

(5) Tác đôi tích phân

$forall gamma in [a,b]Rightarrow int_{a}^{b}f(x)dx=int_{a}^{gamma}f(x)dx+int_{gamma }^{b}f(x)dx$

(6) So sánh giá trị của tích phân

• $f(x)geq 0$ trên đoạn $[a,b]Rightarrow int_{a}^{b}f(x)dxgeq 0$
• $f(x)geq g(x)$ trên đoạn $[a,b] Rightarrow int_{a}^{b}f(x)dxgeq int_{a}^{b}g(x)dx$
• $mleq f(x)leq M$ trên đoạn $[a,b]Rightarrow m(b-a)leq int_{a}^{b}f(x)dxleq M(b-a)$

Ngoài ra còn một vài tính chất tích phân xác định mà các em thường gặp khi làm bài thi mà không thể bỏ qua:

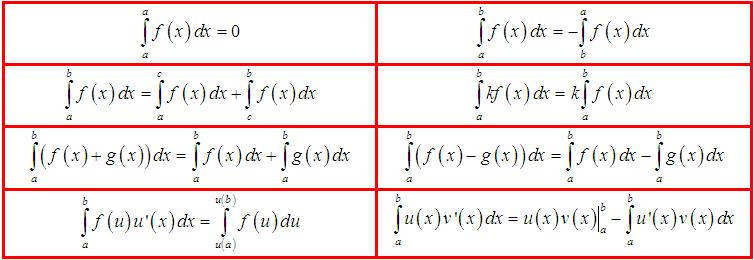
3. Bảng công thức tích phân cơ bản học sinh 12 phải ghi nhớ

Để làm được các dạng bài tập tích phân các em cần lưu và ghi nhớ ngay bảng công thức sau đây:

Đăng ký ngay để được các thầy cô tổng hợp kiến thức tích phân một cách ngắn gọn và dễ hiểu nhất

4. Phương pháp giải các dạng bài tập tích phân

4.1. Phương pháp tích phân từng phần

Nếu u(x) là hàm số có đạo hàm liên tục trên [a;b] thì ta có:

$int_{a}^{b}u(x)v'(x)dc=(u(x)v(x))left|begin{matrix}ba end{matrix}right. -int_{a}^{b}v(x)u'(x)dx$

Hay $int_{a}^{b}udv=uvleft|begin{matrix}baend{matrix}right. - int_{b}^{a}vdu$

Áp dụng công thức trên ta có quy tắc tính $int_{a}^{b}f(x)dx$ bằng phương pháp tích phân từng phần sau đây:

Bước 1: Viết f(x)dx dưới dạng udv = uv'dx bằng cách chọn một phần tích hợp của f(x) làm u(x) và phần còn lại dv=v'(x)dx

Bước 2: Tính du=u'dx và $u=int dv=int v'(x)dx$

Bước 3: Tính $int_{a}^{b}vdu = int_{a}^{b}vu'dx$ và uv$left|begin{matrix}baend{matrix}right.$

Bước 4: Áp dụng công thức $int_{a}^{b}f(x)dx=int_{a}^{b}uvd=uvleft|begin{matrix} baend{matrix}right.-int_{a}^{b}vdu$

4.2. Giải bài tập tích phân bằng cách phân tích

Với phương pháp tích phân từng phần các em có thể sử dụng các đồng nhất các công thức sau đó biến đổi các biểu thức dưới dấu tích phân để trở thành tổng của các hạng tử như sau:

Ví dụ: Tính tích phân $I= int_{2}^{2}frac{x^{2}-2x}{3}dx$

Giải:

Ta có: $I=int_{1}^{2}(frac{1}{x}-frac{2}{x^{2}})dx=(lnleft | x right |+frac{2}{x})left|begin{matrix} 21 end{matrix}right.=(ln2+1)-(ln1+2)=ln2-1$

4.3. Phương pháp tích phân đổi biến số

Với phương pháp biến đổi thì sẽ có 2 dạng và mỗi dạng là một cách tính khác nhau. Cụ thể là:

Dạng 1:

Để tính tích phân: $I=int_{a}^{b}g(x)dx$ ta thực hiện các bước sau đây:

Bước 1: Chọn biến số:

• Phân tích g(x)dx=f[u(x)]u'(x)dx=f[u(x)]d[u(x)]
• Đặt u = u(x)

Bước 2: Thực hiện phép đổi cận

• Với x=a thì u = u(a)
• Với x=b thì u=u(b)

Bước 3: Khi đó ta có $int_{a}^{b}g(x)dx=int_{u^{(a)}}^{u^{b}}f(u)du$

Dạng 2:

Để tính tích phân: $I=int_{a}^{b}f(x)dx$ có hàm số f(x) liên tục trên [a;b], ta làm theo các bước:

Bước 1: Chọn $x=varphi (t)$, trong đó $varphi (t)$ nằm trong tập xác định của f.

Bước 2: Giả sử $varphi '(t)$ liên tục, lấy vi phân dx = dx =$varphi (t)dt$

Bước 3: Ở đây, các em có thể chọn một trong hai cách sau:

- Cách 1: Tính các cận $alpha$ và $beta$ tương ứng theo a và b (điều kiện $a=varphi (alpha$ và $b=varphi (beta )$), khi đó ta được: $I=int_{alpha }^{beta }f(varphi (t).varphi (t)dt$

- Cách 2: Tính theo cách xác định nguyên hàm để tìm ra giá trị của tích phân xác định (lúc này $alpha$ phải là đơn ảnh để thể hiện kết quả của hàm số t thành hàm số của x)

a) Với $I=int_{1}^{1/2}f(x)dx$, lựa chọn ẩn phụ x=sint và $-frac{pi }{2}leq tleq frac{pi }{2}$, ta có thể làm theo cách 1 vì lúc này với x=0 ta có t=0, với $x=frac{1}{2}$ ta có $t =frac{pi }{6}$

b) Với $I=int_{1}^{1/3}f(x)dx$, lựa chọn ẩn phụ x=sint và $-frac{pi }{2}leq tleq frac{pi }{2}$, ta có thể làm theo cách 2 vì lúc này với $x=frac{1}{3}$ sẽ không chỉ ra được số đo góc t.

Nắm trọn kiến thức và phương pháp giải mọi dạng bài tập Toán thi THPT Quốc Gia với bộ tài liệu độc quyền của VUIHOC ngay

4.4. Phương pháp vi phân

Vi phân của hàm số y=f(x) được ký hiệu dy và cho bởi dy=df(x)=y’dx=f’(x)dx

Một số công thức vi phân quan trọng cần phải nhớ:

(1) $dx=frac{1}{a}d(axpm b)=frac{-1}{a}d(bpm ax)$

(2) $xdx=frac{1}{2}d(x^{2}=frac{1}{2a}d(ax^{2}pm b)=-frac{1}{2a}d(bpm ax^{2})$

(3) $x^{2}dx=frac{1}{3}d(x^{3}pm b)=frac{-1}{3a}d(bpm ax^{3})$

(4) $sin x=-d(cosx)=frac{-1}{a}d(a cos xpm b)$

(5) $cos xdx=d(sinx)=frac{1}{a}d(asin xpm b)$

(6) $frac{dx}{cos^{2}x}=d(tanx)=frac{1}{a}d(a tan xpm b)$

(7) $frac{dx}{sin^{2}x}=-d(cotx)=frac{-1}{a}d(acotxpm b)$

(8) $frac{dx}{2sqrt{x}}=d(sqrt{x})=frac{1}{a}d(asqrt{x}pm b)=frac{-1}{a}d(bpm asqrt{x})$

(9) $e^{x}dx=d(e^{x})=frac{1}{a}d(ae^{x}pm b)=frac{-1}{a}d(bpm ae^{x})$

(10) $frac{dx}{x}=d(lnx)=frac{1}{ad(alnxpm b)}=frac{-1}{a}d(bpm alnx)$

>> Xem thêm:

• Các dạng tích phân hàm ẩn cơ bản và bài tập vận dụng
• Cách tính tích phân hàm lượng giác chi tiết và bài tập

5. Phối hợp các phương pháp đối với bài tập dạng nâng cao

Sau khi đã nắm được các phương pháp giải bài tập tích phân thì dưới đây sẽ là một vài ví dụ:

Để ôn tập nhiều dạng bài về tích phân, các em cùng thầy Thành Đức Trung tổng ôn và luyện đề các bài tập nguyên hàm tích phân nhé! Trong video này, thầy Trung sẽ có rất nhiều mẹo giải hay, các bấm máy CASIO giải tích phân cực nhanh.

Trên đây là toàn bộ công thức và các dạng bài tập về tích phân thường gặp thuộc chương trình Toán 12. Tuy nhiên nếu em muốn đạt kết quả tốt thì hãy ôn tập nhiều công thức toán 12 và làm thêm các dạng bài khác nữa. Em có thể truy cập Vuihoc.vn và đăng ký tài khoản để luyện đề! Chúc các em đạt kết quả cao trong kỳ thi THPT Quốc Gia sắp tới.

>> Xem thêm:

• Đầy đủ và chi tiết bài tập phương trình logarit có lời giải
• Tuyển tập lý thuyết phương trình logarit cơ bản
• Công thức tính nguyên hàm từng phần và cách giải bài tập
• Tính nguyên hàm tanx bằng công thức cực hay
• Tích Phân Từng Phần: Phương Pháp Tính, Ví Dụ Và Bài Tập Minh Họa